by Stefano Serafini
An important principle of biourbanism is that nature and culture do not belong to separated aims but interact on a common ground, whose center is the human body.
After the great influence of Robin George Collingwood and of his idealism (Collingwood, 1958), 20th century critics tended to regard art and architecture as a strictly intellectual subject. The discovery of mirror neurons, on the contrary, witnessed that the visual experience of environments, objects, and depictions is at once always emotional and cognitive, and that every representation activates neuro-motor circuits. The so-called “neuroaesthetics” studies the phenomenon of the artistic representation with the support of the functional magnetic resonance imaging (fMRI). Such a technique shows, for instance, that looking at a representation of a suffering person activates the brain networks normally involved when the observer himself feels pain. Certain abstract pieces of art, e.g. Lucio Fontana’s “cuts”, stimulate the circuits that coordinate the same body movement the artist did while creating his work. On the other hand, the observation of Michelangelo’s “unfinished” Slaves (Prigioni) triggers neural discharges in the very same cortex areas connected to the movement of the body parts that seem to be struggling for setting themselves free from the marble (Freedberg & Gallese, 2007; Ramachandran & Rogers-Ramachandran, 2006). According to Vittorio Gallese, in fact human beings come to know the outer world by mirroring it into the dynamics of their own body. Such an “embodied simulation” generates an “intentional consonance” which autistic subjects typically lack (Gallese, 2003; 2006).
The isomorphic resonance involves the whole organism along with its intentional, cognitive, and emotional processes on an objective neurological basis. Physical-mathematical optima, the same that rule the physical, biological, and neural order measure such objectivity.
Evolution in biology has come a long way during the last decades, following the discovery and affirmation of auto-evolution and the laws of forms (Gould & Lewontin, 1979; Lima-de-Faria, 1988; 2012; 2017; Denton, Marshall, & Legge, 2002; Stewart, 2003; Gielis, 2003; Brown, West, & Enquist, 2005; Fodor & Piattelli-Palmarini, 2010). The role of chance and natural selection has been dramatically reconsidered, opening the gate to the second great revolution of the Darwinian model corresponding to the radical change that happened in physics after the advent of nonlinear dynamics of complex systems (Depew & Weber, 1995; 1996). Even genes have lost a great share of their centrality as axes of transmission of evolution because it is the physical-mathematical constraint (long before genes) that canalizes their function into the organization of the form (Lima-de-Faria, 1988). Unfortunately, Kaplan missed such information when, during his research on biophilia, he thought of referring to the primeval environment of the savannah as a ground for human design preferences (Kaplan, 1987). According to this author, human beings would feel attracted by certain forms because they recall the original African environment where our species has evolved. In fact the foundation has to be structural rather than historical, and it seems that it can be explained by cognitive reasons (Salingaros, 2010), possibly based on the homorphism between the brain structures and the environment after the so-called “laws of form” (Piattelli-Palmarini, 2006).
Notoriously, fractal features are common in nature (Hagerhall, Purcell, & Taylor, 2004; Taylor, 2006; Taylor, Newell, Spehar, & Clifford, 2005). These in turn are connected to the Fibonacci number and the golden rule (Snijders, 1993), i.e. the number that is the limit to n that tends to the infinite of the ratio P(n+1)/P(n) among two consecutive Fibonacci numbers.
The result is the outstanding presence of geometrical details in natural objects ordered in a self- similar and densely scaled way, e.g. arborescent structures such as trees, river deltas, lightning structures, or the rhythm of sea waves and of mountains peaks. René Thom, with his pioneering works, has shown that all natural phenomena share a substantially mathematical character (Thom, 1980; 1991, p. 77).
Studies partly explained the impressive spread of the Fibonacci series in nature with its optimality, for example in both phyllotaxis’ packing and unfolding (Crompton, 2005). Seeds, petals, and leaves are packed and unfold in space with a constant angle of 0,618034… (or 222,492…°). Thus there will be 1,618… leaves at every turn (or 0,618… turns for each leaf), which means the best possible exposition to light with the less shadow from the above leaves—a splendid example of translation of a morphogenetic process into the morphofunctional level (Douady & Couder, 1993).
Finally, Adrian Bejan opened up a new field of studies after the discovery of the “constructal law” that unites the living and the unliving worlds by defining the time direction of all evolutionary design phenomena, based on a constant facilitation of flow access (Bejan & Zane, 2012). Shapes of things—no matter if artificial or natural—exist because they obey the flowing dynamic that shaped them by functioning through them. Think of the feature of an ocean wave. Its form is the result of a flow obeying the material constraint of a fluid pushed from wind into air. Design is intrinsic to the organization of matter, and the morphofunctional level of biology, including its periodicity, lies in the molecular and atomic level, as Lima-de-Faria puts it in his revolutionary works about evolution (Lima-de-Faria, 1988; 2012; 2017).
If one can be amazed by the constant presence of Fibonacci and prime numbers in nature, expression of a self-organizing morphogenesis (Douady & Couder, 1996), more impressive is the discovery of universal patterns and “spontaneous” irrational algorithms in geopolitics (Lotman, 1990, especially pp. 191–202), poetry (Duckworth, 1962; Pötters, 1987), music (Snijders, 1993), mythology (De Santillana & von Dechend, 1969), and linguistics (Carnie, Medeiros, & Boeckx, 2005; Soschen, 2006). How it is possible, if the free will of man is supposed to have created them?
Biourbanism, after Salingaros, has focused on the geometrical features in spontaneous urban environments and buildings. Biophilic architecture—from Bushmen huts to European Gothic—has in fact the structure of an authentic living language. It is organic, auto-similar, full, and coherent on every scale (Crompton, 2002), capable of bringing emotional and cognitive regeneration. So does the so-called “everyday urbanism” (settlements without urban planners), which exhibits an instinctive use of universal scales. Goldberger speculated that the fractality of Gothic architecture expresses some patterns of the organization of our brain (Goldberg, 1996) and found that fractal dynamics are an important indication of physiological health, e.g. in the cardiac rhythm (Goldberg et al., 2002). Yannick Joye thinks that fractal forms are effective in art therapy (Joye, 2006). Frances Kuo and William Sullivan noticed that when built environments lack natural features they trigger aggressiveness (Kuo & Sullivan, 2001; Kaplan, 1987b).
On the ground of researches that connect neurology and linguistics, besides general observations on the nature of the context (Lotman, 1990), we could link this biophilic design to natural languages. According to Salingaros (2010), anti-language design is usually achieved through anti-patterns, i.e. anti-structures unfolded from the deliberate destruction of natural patterns.
Piattelli-Palmarini and Uriagereka (2008) unveiled some algorithms at the basis of human language and offered some valid elements to sustain the hypothesis of a direct relation between the structure of language and the morphogenetic order of the neurophysiological structure. Here, I will try to reflect on such a match by confronting the results of their research to a seemingly unrelated work carried out by Christopher Alexander half a century ago.
Alexander and colleagues arranged a series of interesting experiments at the Center for Cognitive Studies, Harvard University during the 60s aimed at measuring the perceived coherence of patterns. Coherence was defined in operational terms as perceptual agility (Alexander & Huggins, 1964; Alexander & Carey, 1968; Alexander, 2002–2005, vol. 1, pp. 186–194; 449–457) and followed the concept of “center”.
According to Alexander, a “center” is an entity that, for geometrical and functional reasons, resonates with our perception, making a pattern “alive” (Alexander, 2002–2005, vol. 1, pp. 83–85). The more a place or an object exhibits centers, the more it feels alive and attractive to people. Overlapping local symmetries (distinct unities of symmetry within a whole) tend to produce centers and enforce the character of wholeness of the object or space within which they occur. For example, the façade of the Zeppelinfield by Albert Speer with its monstruous and violent overall geometry lacks such a quality, which instead is abundant in the complex of the Alhambra in Granada, where the overall geometry is missing yet thousands of local symmetries rule the scene (Ibidem, 186–188).
As test material, the researchers produced 35 paper strips composed of 7 squares. Four of these squares were white, and 3 were black. The 35 patterns represented in the strips filled every possible reciprocal space combination (segments) of the 7 squares when connected.
The strips were given to different subjects for them to rank their “coherence” as patterns, and the results were significant: the “coherence” rank order tended to be roughly the same according to every different observer (see Figure 3). The correlation did not change by administering the test in different modalities. No matter if subjects were questioned about individuating the pattern “with more coherence”, or “with more structure”, or “the quickest to be recognized”, or “the easiest to remember”, or “the easiest to describe in words”. The recognition of coherence came out to be a very stable variable also when shifting to different cognitive processes. The same occurred when changing subjects. In the end, it is a matter of ease of perception, i.e. of rules in human cognitive processing or gestalt, and the result is no surprise.
It took four years of study, however, to understand that the coherence perceived by the subjects in the experiment depends on the number of local symmetries or subsymmetries that are present in the pattern and not on the lumpiness or the overall symmetry of the object. The latter contain the subsymmetries, which result as “hidden” because we are rationally used to focusing on the “major” features of an object. This was also true in the case of the extreme simplicity of the material used for the test.
Despite local subsymmetries are often far from being evident at first sight, Alexander found that in fact subsymmetries work as a “glue”. The more subsymmetries, the more solid and coherent is the resulting space or object. The more subsymmetries overlap, the stronger the glue, which is the more the space shows the quality of “wholeness” (or W). For making it easy to measure such a wholeness, Alexander proposed the following function, where Si means subset and Csymm means coherence (“life”) of a given set R (in the specific experiment, the pattern):
0 if Si is not connected
Csymm(Si) = 1 if Si is connected and bilaterally symmetrical
0 if Si is connected but not bilaterally symmetrical
In other words, the locally symmetric connected sets stand out as the strongest centers of R (Alexander, 2002–2005, vol. 1, p. 450).
The number of values Si equal 1 in a given set R indicates the value of the “wholeness” (Wsymm). Now, Wsymm has a predictive power about the way a set R will be experienced. The formula needs some adjustments, and the Author indicates two specific patterns: WBWBBBWW and BWWBWWB (where W means white and B black). These configurations work as centers despite they lack symmetry, i.e. people recognize them as wholeness but the function Wsymm does not. Nevertheless, the approximation is so good that the function Wsymm is able to foresee (and partly explain) the way we experience patterns as wholes. Then, the approximation has been the subject of ulterior refinements (Salingaros, 1997; Klinger & Salingaros, 2000).
The fact that we can often miss the “wholeness” because of the rigid mindset imposed on cognition by our logocentric education reminds us of the teaching by Edmund Husserl (1954). The incapability of being non-judgmental (Husserl’s epoché) misleads our focus from certain characteristics of the experience toward others. Alexander suggests that it is exactly such a bias on perception of wholeness that is the main cause of so many architectural disgraces, where an intellectual superimposition interferes with the natural flowing of the cognitive process. Such a cognitive bias, according to the observations of the Author, especially characterizes adults and averagely educated people, not children nor mentally disabled persons (Alexander, 2002–2005, vol. 1, pp. 453–454). People schooled according to our logocentric and mechanistic culture, therefore, tend to miss the “wholeness” and to catalogue perceptual sets according to pre-formed, abstract, and arbitrary categories that do not match what Alexander calls “life”.
Let us now go to the biolinguistics research by Piattelli-Palmarini and Uriagereka (2008). These two authors also noticed the existence of optimal organizational patterns consisting of cognitively significant subsystems. They ground their work on the existence of relevant morphogenetic structures in biophysics, and manage to apply such an evidence to linguistic behavior. First, thus, they focus on the recurrence of the golden ratio in the ontology of phonological syllables.
Not many people know that the set of vowels (V) and consonants (C) of every known language always follows a pattern of decreasing recurrence (Blevins, 1995), as below:
CV (and its stressed variant CVV)
CVC (and its stressed variant CVVC)
V
C
Languages do not recognize/accept templates as, for example, CVVVC or VVC. The above variants in parentheses appear only seldom and can be explained in terms of nuances of consonantic groups or vocalic coloritures. Some languages, such as Native American Klamath or Vietnamese Sedang keep the same pattern with the only difference that they do not have syllables without an onset (V(C)). Only a few languages work with just units CV, for example the indigenous Peruvian Arabela.
On the basis of this, it is possible to generate a binary optimizing algorithm, which Piattelli- Palmarini and Uriagereka call F because the number of its possible combination grows according to the Fibonacci series (Figure 1).
In the algorithm, the sign (–) means spaces and the sign (+) means boundaries:
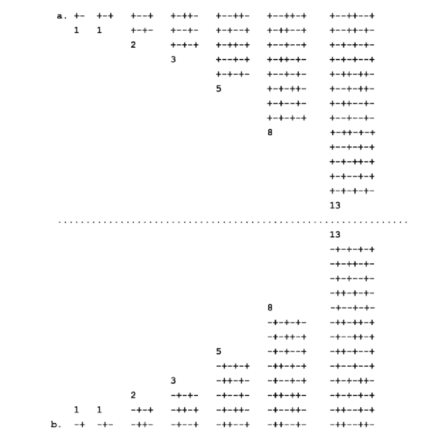
As one can see, the series of spaces and boundaries obey a Fibonacci pattern, namely:
1, 1, 2, 3, 4, 8, and 13
The rules that produce such a curious development are simple:
i) Beginning with either a + or a –
ii) Concatenating it to another + or a –, at the condition of
iii) Avoiding to combine identical symbols unless they are adjacent to a different symbol.
We can transform the above into linguistic rules, as follows (Piattelli-Palmarini & Uriagereka, 2008, p. 212):
i) Nucleus constraint: look for a maximal space. Then,
ii) Onset constraint: try to assign an onset boundary to that space. Then,
iii) Coda constraint: try to assign a coda boundary to that space.
The consequence is the following:

It is rather evident that six groups emerge:
a. + – ; b. + – – ; c. + – + ; d. + – – + ; e. – ; f. – +
If we substitute the symbols (–) and (+) with (V)owel and (C)onsonant, they become:
CV 37 37
(and its stressed variant CVV) 11 7
CVC 21 17
(and its stressed variant CVVC) 10 8
V 0 19
VC 0 13
The scheme is identical to the one given above about the occurrence of vowels and consonants combinations in every human language. The numbers to the right express the actual recurrences of the algorithm that started with an onset boundary and those that started with a space.
Let us now compare these results with those obtained by Alexander and colleagues, as presented in Figure 3. Every possible pattern of the strips are here in order from the one with more subsymmetries to the one that has less subsymmetries (Wsymm). The maximum Wsymm value is 9 (above left), the minimum 5 (below right). If we compare this to the result by Piattelli-Palmarini and Uriagaereka, we find that their F game has generated sets with value 1 (“connected and bilaterally symmetrical”). The cognitive structural emergent property of the linguistic recognizability/acceptability of the syllables matches the bilateral subsymmetry that characterizes the centers of Alexander.
It is clear that we can formally compare only one out of the 16 columns of the F game to the set of strips given by Alexander, i.e. the sixth column, which is also the one composed by 7-element strings.

Therefore, here we are with 8 sets:
a. + – – + – – +
b. + – – + – + –
c. + – + – – + –
d. – + – + – + –
e. – + – + – – +
f. – + – – + – +
g. – + – – + + –
h. – + + – – + –
That is, by appropriately replacing the signs:
a. CVV CVVC (7 subsymmetries)
b. CVV CV CV (6 subsymmetries)
c. CV CVV CV (6 subsymmetries)
d. V CV CV CV (9 subsymmetries)
e. V CV CVVC (6 subsymmetries)
f. V CVV CVC (6 subsymmetries)
g. V CVVC CV (5 subsymmetries)
h. VC CVV CV (5 subsymmetries)
This set produces the following frequency values:
- For the sets beginning with (+) or C:
CV 4 occurrences
CVV 3 occurrences
CVVC 1 occurrence
- For the same beginning with (–) or V:
CV 6 occurrences
V 4 occurrences
CVV 2 occurrences
CVVC 2 occurrences
CVC 1 occurrence
VC 1 occurrence
- For all the sets:
CV 10 occurrences
CVV 5 occurrences
V 4 occurrences
CVVC 3 occurrences
CVC 1 occurrence
VC 1 occurrence
The match is striking. We can see the emergence of a structuration of cognitive “preferences” after order and frequency, congruent to the linguistic “preferences” that spontaneously self-organize in human languages. One could repeat the Alexander experiment with longer strips that allow for matching all the 16 columns of the F game, but this seems enough to me for showing an example of isomorphic patterns emergence in two distinct processes involving linguistics and design. Both of these processes lie in “cultural” but at the same time radically “natural” phenomena.
These morphogenetic patterns emerge in design, like in language, as subcodes rather than proscriptions. Biopractice in design is a repository and a creative forge of generative (connective) acts and rules that refer to and use these subcodes. It finds and respects the conditions of matching languages that in turn could be well unlimited in number. The presence of subcodes can be the mark of a design that performs well in relation to the environment, health, neuroergonomics, et cetera, because its order is likely to match the same constraints that it shares with the environment, our body, and our nervous system.
Design that instead breaks these patterns may feel as a linguistic “mistake” and a stressing improper element that the organisms refuse. Anti-language design is thus not a matter of style but of disconnection from these “hidden” subcodes.
REFERENCES
Alexander, C. (2002–2005). The nature of order (Vols. 1–4). Berkeley, CA: Center for Environmental Structure.
Alexander, C., & Carey, S. (1968). Subsymmetries. Perception and Psychophysics, 4(2), 73–77.
Alexander, C., & Huggins, B. (1964). On changing the way people see. Perceptual and Motor Skills, 19, 235–253.
Bejan, A., & Zane, J. P. (2012). Design in nature: How the constructal law governs evolution in biology, physics, technology, and social organizations. New York: Doubleday.
Blevins, J. (1995). The syllable in phonological theory. In J. Goldsmith (Ed.), The handbook of phonological theory. (pp. 206–244). Oxford: Blackwell.
Brown, J. H., West, G. B., & Enquist, B. J. (2005). Yes, West, Brown and Enquist’s model of allometric scaling is both mathematically correct and biologically relevant. Functional Ecology, 19, 735–738.
Carnie, A., Medeiros, D., & Boeckx, C. (2005). Some consequences of natural law in syntactic structure. Unpublished manuscript, University of Arizona and Harvard University, USA. Retrieved from http://dingo.sbs.arizona.edu/~carnie/publications/PDF/BoeckxCarnie Medieros.pdf
Collingwood, R. G. (1958). The principles of art. New York: Oxford University Press.
Crompton, A. (2002). Fractals and picturesque composition. Environment and Planning B, 29, 451–459.
Crompton, A. (2005). Scaling in a suburban street. Environment and Planning B: Planning and Design, 32(2), 191–197.
Denton, M. J., Marshall, C. J., & Legge, M. (2002). The protein folds as platonic forms: New support for the pre-Darwinian conception of Evolution by natural law. Journal of Theoretical Biology, 219, 325–342.
Depew, D. J., & Weber, B. H. (1995). Darwinism evolving: Systems dynamics and the genealogy of natural selection. Cambridge, MA: The MIT Press.
Depew, D. J., & Weber, B. H. (1996). Natural selection and self-organization. Biology and Philosophy, 11(1), 33–65.
De Santillana, G., & von Dechend, H. (1969). Hamlet’s mill. Boston: Gambit.
Douady, S., & Couder, Y. (1992). Phyllotaxis as a self-organized growth process. Physical Review Letters, 68(13), 2098–2101.
Douady, S., & Couder, Y. (1996). Phyllotaxis as a self-organizing process. Part I: The spiral modes resulting from time-periodic iterations. Journal of Theoretical Biology, 178(1996), 255–273.
Duckworth, G. E. (1962). Structural patterns and propositions in Virgil’s Aeneid: A study in mathematical composition. Ann Arbor, MI: The University of Michigan Press.
Fodor, J., & Piattelli-Palmarini, M. (2010). What Darwin got wrong. London: Profile Books.
Freedberg, D., & Gallese, V. (2007). Motion, emotion and empathy in esthetic experience. Trends in Cognitive Sciences, 11(5), 197–203.
Gallese, V. (2003). The roots of empathy: The shared manifold hypothesis and the neural basis of intersubjectivity. Psychopathology, 36(4), 171–180.
Gallese, V. (2006). Intentional attunement: A neurophysiological perspective on social cognition and its disruption in autism. Experimental Brain Research/Cognitive Brain Research, 1079, 15–24.
Gielis, J. (2003). A generic geometric transformation that unifies a wide range of natural and abstract shapes. American Journal of Botany, 90, 333–338.
Goldberger, A. L. (1996). Fractals and the birth of Gothic: Reflections on the biologic basis of creativity. Molecular Psychiatry, 1, 99–104.
Goldberger, A. L., Amaral, L. A. N., Hausdorff, J. M., Ivanov, P. C., Peng, C. K., & Stanley, H. E. (2002). Fractal dynamics in physiology: Alterations with disease and aging. Proceedings of the National Academy of Sciences, 99(1), 2466–2474.
Gould, S. J., & Lewontin, R. C. (1979). The spandrels of San Marco and the panglossian paradigm: A critique of the adaptationist programme. Proceedings of the Royal Society of London, Series B, 205(1161), 581–598.
Joye, Y. (2006). Some reflections on the relevance of fractal art for art therapy. The Arts in Psychotherapy, 33, 143–147.
Hagerhall, C. M., Purcell, T., & Taylor, R. (2004). Fractal dimension of landscape silhouette outlines as a predictor of landscape preference. Journal of Environmental Psychology, 24, 247–255.
Kaplan, S. (1987). Aesthetics, affect and cognition: Environmental preference from an evolutionary perspective. Environment and Behavior, 19, 3–32.
Kaplan, S. (1987b). Mental fatigue and the designed environment. In J. Harvey & D. Henning (Eds.), Public environments (pp. 55–60). Washington, DC: EDRA.
Klinger, A., & Salingaros, N. A. (2000). A pattern measure. Environment and Planning B: Planning and Design, 27, 537–547.
Kuo, F. E., & Sullivan, W. C. (2001). Aggression and violence in the inner city: Effects of environment via mental fatigue. Environment and Behavior, 33(4), 543–571.
Lima-de-Faria, A. (1988). Evolution without selection: Form and function by autoevolution. London/New York/Amsterdam: Elsevier Science.
Lima-de-Faria, A. (2012). Molecular geometry of body patterns in birds. Heidelberg: Springer.
Lima-de-Faria, A. (2017). Periodic tables unifying living organisms at the molecular level: The predictive power of the law of periodicity. Singapore: World Scientific.
Lotman, J. M. (1990). Universe of the mind: A semiotic theory of culture. Bloomington: University of Indiana Press.
Piattelli-Palmarini, M. (2006). The return of the laws of form. In C. P. Manzù (Ed.), Life on the edge (pp. 45–57). Rome: Centro Pio Manzù.
Piattelli-Palmarini, M., & Uriagereka, J. (2008). Still a bridge too far? Biolinguistic questions for grounding language on brains. Physics of Life Reviews, 5, 207–224.
Pötters, W. (1987). Chi era Laura? Strutture linguistiche e matematiche nel Canzoniere di Petrarca [Who was Laura? Linguistic and mathematical structures in Petrarca’s Canzoniere]. Bologna: Il Mulino.
Ramachandran, V. S., & Rogers-Ramachandran, D. (2006). The neurology of aesthetics. Scientific American Mind, 17(5), 16–18.
Salingaros, N. A. (1997). Life and complexity in architecture from a thermodynamic analogy. Physics Essays, 1(10), 165–173.
Salingaros, N. A. (2009). Antiarchitettura e demolizione [Antiarchitecture and demolition]. Florence: Libreria Editrice Fiorentina.
Salingaros, N. A. (2010). Twelve lectures on architecture: Algorithmic sustainable design. Solingen: Umbau Verlag.
Snijders, C. J. (1993). La sezione aurea. Arte, natura, matematica, architettura e musica [The golden ratio in art, nature, architecture, and music]. (Red./studio redazionale, Trans.). Como: Franco Muzzio.
Soschen, A. (2006). Natural law: The dynamics of syntactic representations in MP. In H. Broekhuis & R. Vogel (Eds.), Optimality theory and minimalism: A possible convergence? Linguistics in Potsdam, 25, 43–76.
Stewart, I. (2003). Self-organization in evolution: A mathematical perspective. Philosophical Transaction of the Royal Society of London A, 361, 1101–1123.
Sullivan, L. H. (1896, March). The tall office building artistically considered. Lippincott’s Magazine, 403–409.
Taylor, R. P. (2006). Reduction of physiological stress using fractal art and architecture. Leonardo, 39(3), 245–251.
Taylor, R. P., Newell, B. R., Spehar, B., & Clifford, C. W. G. (2005). Fractals: A resonance between art and nature? In M. Emmer (Ed.), Mathematics and culture II: Visual perfection (pp. 53–63). Berlin: Springer-Verlag.
Thom, R. (1980). Modèles mathématiques de la morphogénèse [Mathematical models of morphogenesis]. Paris: Christian Bourgeois.
Thom, R. (1991). Esquisse d’une sémiophysique [A sketch of semiphysics]. Paris: InterEditions.
Originally published in the epistemology of design issue of the Journal of Biourbanism Volume V, 1&2/2016